※次の解答はただの参考です。必ず自分で探求した後で解答を読むことにしましょう。

【ポイント】

この方程式は，絶対値を含む方程式ですね。絶対値の式を解くときに，まずは絶対値の符号をはずしておきます。中身の符号により，場合を分けて考えます。

【出題領域】

数と式。この問題を完璧に解くために，以下の知識が必要です。

（１）絶対値を含む方程式の解き方
（２）2次方程式の解き方
（３）無理数の整数部分・小数部分
（４）１次不等式の解き方

【絶対値記号を含む方程式・不等式を解く手順】

STEP①：絶対値記号の中身が0以上か負かで場合分けをし，絶対値の記号をはずす。
STEP②：普通に方程式・不等式を解く
STEP③：場合分けの条件を満たすかどうかを確認する
STEP④：解をまとめる。です。この手順に従って解いていきましょう。

【解答】

（１）方程式①の絶対値を外して      

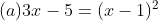
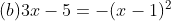
(a)を解いて

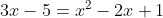
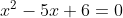
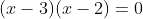
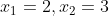
　(b)を解いて

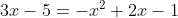
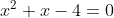
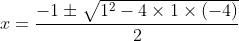
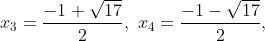
（１）の条件に満たす解は

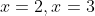
である。

---

（２）（１）より，方程式①の解は

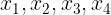
全部で４個ある。mの範囲を求めるので，mをαで表していく。条件

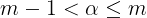
より，

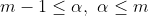
すなわち

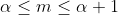
を得る。次はαの値を調べればよい。すなわち，方程式①の解のうちで最小のもの

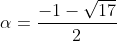
の範囲を調べる。

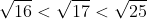
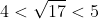
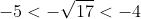
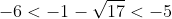
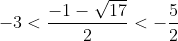
つまり

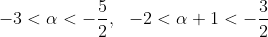
数直線で示すと

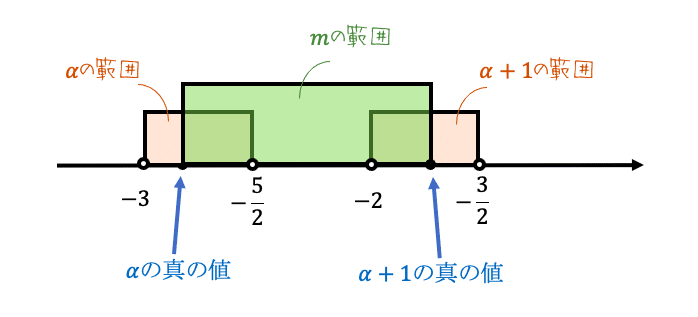
整数mは-2しか取れない。

別の方法もあります，よかったら自分の考え方をコメント欄へどうぞ。

【正解】

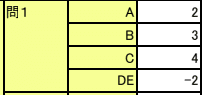
解答部分は自作なので，著作権を放棄しておりません。記事をSNS等へシェアしていただけたらすごく嬉しいですが，内容だけを複写・複製・翻訳することは固くお断りします。皆様のご協力をよろしくお願いいたします。

2010年第1回数学コース１の他の問題を見にいく

---

• Twitter

コミュニケーションボックス