※次の解答はただの参考です。必ず自分で探求した後で解答を読むことにしましょう。

【ポイント】

問題の流れに従って考えてみよう。まず（１）において，与えられた式から平方完成へ。

【出題領域】

数と式，集合と命題。この問題を完璧に解くために，せめて以下の知識が必要です。

（１）平方完成の方法
（２）必要条件と十分条件

この２つの項目を簡単にまとめました。

【平方完成の手順】

平方完成は以下の手順で行う。

【必要条件・十分条件の見方】

まず，必要条件・十分条件の定義をもう一度確認しよう。

簡単に言うと，主語が統一されて，矢印の左に書く場合，右矢印（⇒）は十分条件，左矢印（⟸）は必要条件となります。例えば，

また，真偽の調べ方も重要ですね。その点の復習については，また別の記事をご覧ください。

ではでは，問題を解いてみよう。

【解答】

（１）平方完成して

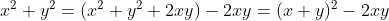
（式①）を得る。
条件（b）のとき，すなわち

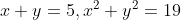
のとき，式①は

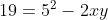
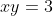
が得られる。条件（c）のとき，すなわち

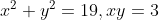
のとき，式①は

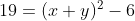
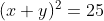
になる。つまり，

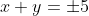
が得られる。

---

（２）（１）により，条件（b）のとき，

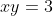
が得られるため，条件（a）と（c）が成り立つ（真）。
条件（c）のとき，

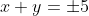
が得られるため，条件（a)と条件(b)が成り立たない（偽）。
続いて式①を用いて条件(a)のときを考察する。
条件(a)のとき，すなわち

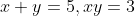
のとき，式①は

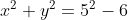
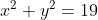
が得られ，条件（b）と条件（c）が成り立つ（真）。
まとめて言うと

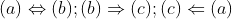
がある。つまり，
　　条件（a）は（b）であるための⓪必要十分条件である
　　条件（b）は（c）であるための①十分条件であるが，必要条件ではない
　　条件（c）は（a）であるための②必要条件であるが，十分条件ではない

【正解】

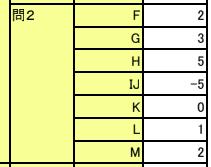
解答部分は自作なので，著作権を放棄しておりません。記事をSNS等へシェアしていただけたらすごく嬉しいですが，内容だけを複写・複製・翻訳することは固くお断りします。皆様のご協力をよろしくお願いいたします。

2010年第1回数学コース１の他の問題を見にいく

---

• Twitter

コミュニケーションボックス