※次の解答はただの参考です。必ず自分で探求した後で解答を読むことにしましょう。

【ポイント】

5個の異なる数字から4個の数字を取り出し，そして並べるわけですね。注意すべきなことは，最高位には0を置いてはいけません。

【出題領域】

場合の数と確率。この問題を完璧に解くために，せめて以下の知識が必要です。

（１）和の法則と積の法則
（２）組み合わせと順列

ではでは，問題を解いてみよう。

【解答】

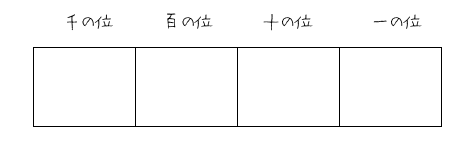
（１）
step1：千の位は，0を除く1〜4の数から１個を取るから，4通り。
step2：そのおのおのについて，百，十，一の位は，0を含めた残りの4個の数字から３個を取る順列で，

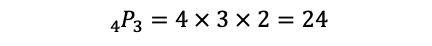
通り。よって，求める個数は

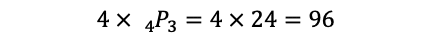
個ある。このうち，0を使わないものなら，step2において，0を除いた残りの3個の数字から３個を取る順列で，

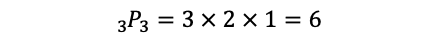
通り。よって，0を使わないものは

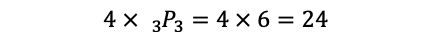
個ある。

---

（２）同じ数字を何度も使っても良ければ，
step1：千の位は，0を除く1〜4の数から１個を取るから，4通り。
step2：そのおのおのについて，百，十，一の位は，5個の数字から自由に取る順列で，

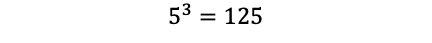
通り。よって，求める個数は

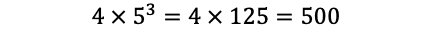
個ある。
　（i）１と３を２個ずつ使うものは，以下の6通りある。

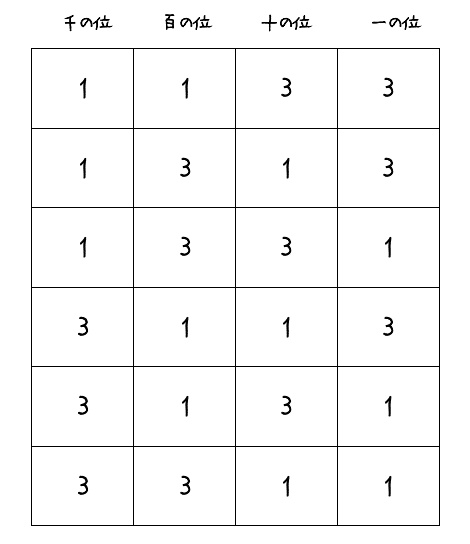
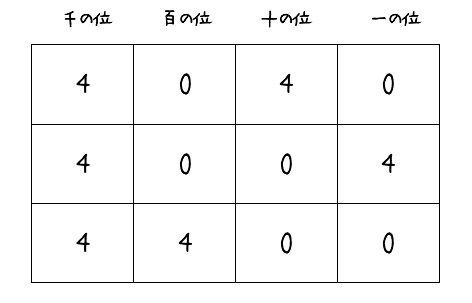
　（ii）0と4を２個ずつ使うものは，以下の3通りある。

　（iii）iとiiのヒントを受けて2つの数字を2個ずつ使うものは，同じく0を使うパターンと0を使わないパターンを分けて考えよう。
　　0を使わない場合，1〜4の数から２個取り出す場合の数は，

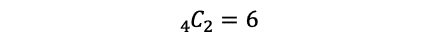
　　（i）により，１種類の組み合わせに対して，求める数は6通りあるので，計

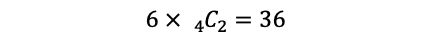
　　個ある。
　　0を使う場合，1〜4の数から1個取り出す場合の数は，4通りで，（ii）により，１種類の組み合わせに対して，求める数は3通りあるので，計

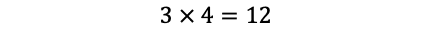
　　個ある。よって，２つの数字を２個ずつ使うものは全部で48個ある。

【正解】

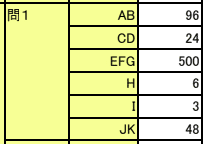
解答部分は自作なので，著作権を放棄しておりません。記事をSNS等へシェアしていただけたらすごく嬉しいですが，内容だけを複写・複製・翻訳することは固くお断りします。皆様のご協力をよろしくお願いいたします。

2010年第1回数学コース１の他の問題を見にいく

---

• Twitter

コミュニケーションボックス