※次の解答はただの参考です。必ず自分で探求した後で解答を読むことにしましょう。

【ポイント】

sin𝜃, cos𝜃, tan𝜃 のうち1つでも値がわかれば，三角比の相互関係から残りの2つの値を求めることができます。

【出題領域】

図形。この問題を完璧に解くために，せめて以下の知識が必要です。

（１）三角比の相互関係
（２）余弦定理，三平方の定理
（３）正弦定理
（４）三角形の面積の求め方

詳しく言うと，

【三角比の相互関係】

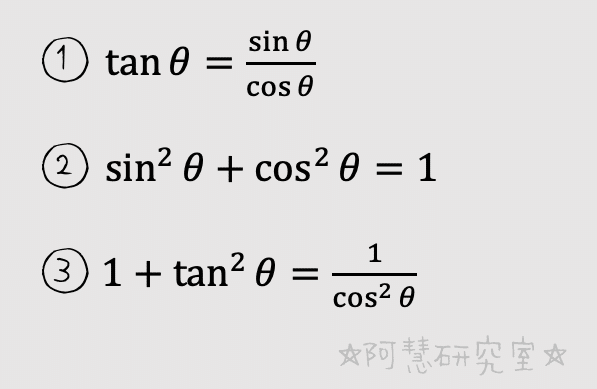
【余弦定理・三平方の定理・正弦定理】

という三角形に関するすごく重要な結論ですね。ぜひ身に付けてください。さてと，問題を解いてみよう。

【解答】

まず，三角比の相互関係

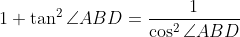
より，

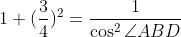
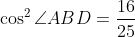
三角形ABDは鋭角三角形だから，

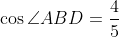
が得られる。そして，余弦定理により，三角形ABDにおいて，

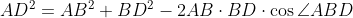
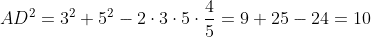
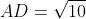
また，三角比の相互関係

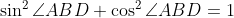
より，

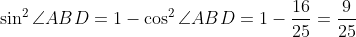
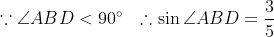
が得られる。さらに，BCは三角形ABDの外接円の直径だから，正弦定理により，

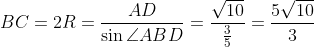
が得られ，直径に対する円周角は直角なので，三平方の定理により，

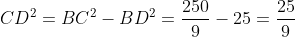
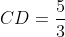
が得られる。
四角形ABCDの面積Sは，三角形ABDと三角形BDCの面積の和だから，

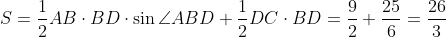
である。

【正解】

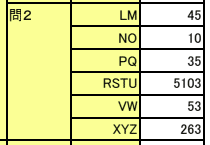
解答部分は自作なので，著作権を放棄しておりません。記事をSNS等へシェアしていただけたらすごく嬉しいですが，内容だけを複写・複製・翻訳することは固くお断りします。皆様のご協力をよろしくお願いいたします。

2010年第1回数学コース１の他の問題を見にいく

---

• Twitter

コミュニケーションボックス