※次の解答はただの参考です。必ず自分で探求した後で解答を読むことにしましょう。
【ポイント】
数と式。式の整理,展開に焦点を当てた問題です。難しい問題ではないので,直接に解いていきましょう!
【出題領域】
数と式。式の整理,展開に焦点を当てた問題です。難しい問題ではないので,直接に解いていきましょう!
【解答】
問題文に従って,まず,②よりyをx用いて表すと
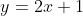
(式④)となり,①よりzをx用いて表すと
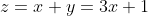
(式④)となる。
次に,式④を式③に代入して,
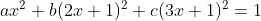
となり,展開して降べきの順に整理すると
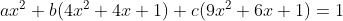
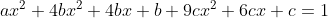
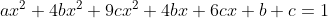
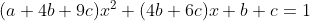
となる。この式はすべてのxに対して成り立つから,x=0,x=1,x=ー1を代入しても成り立つ。よって,
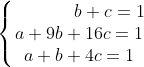
を得る。よって,これらをa,b,cの連立方程式とみて解くと
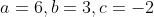
である。

【正解】
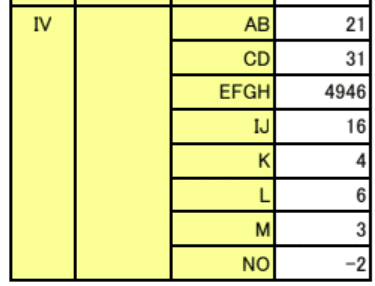

解答部分は自作なので,著作権を放棄しておりません。記事をSNS等へシェアしていただけたらすごく嬉しいですが,内容だけを複写・複製・翻訳することは固くお断りします。皆様のご協力をよろしくお願いいたします。
2010年第1回数学コース1の他の問題を見にいく
コミュニケーションボックス


