※次の解答はただの参考です。必ず自分で探求した後で解答を読むことにしましょう。

【ポイント】

問（１）は箱から９枚のカードを２枚同時に取り出す。→組み合わせ
問（２）は取り戻すパターンになり，毎回の試行は独立であり，何回繰り返すことになります→重複試行。

【出題領域】

場合の数と確率。この問題を完璧に解くために，せめて以下の知識が必要です。

（１）場合の数（組み合わせ）
（２）期待値
（３）独立試行
（４）重複試行
（５）和事象とその確率，排反事象とその確率

【期待値の意味とその計算】

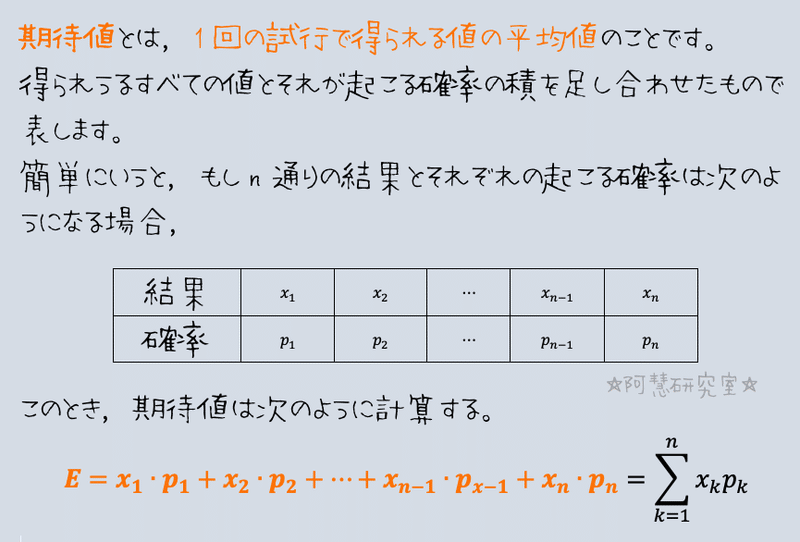
【解答】

（１）１〜９が書かれた９枚のカードから２枚を同時に取り出す場合の数は

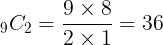
取り出したカードに書かれた数の和Sが５以下となる場合は

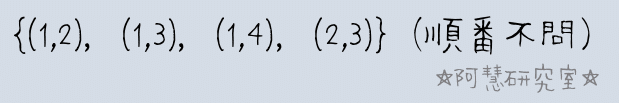
の４通りある。よって，

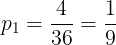
Sが５以下のときは得点として10-S，Sが５より大きいときは得点として2を与えるため，次のように点数を振ります。

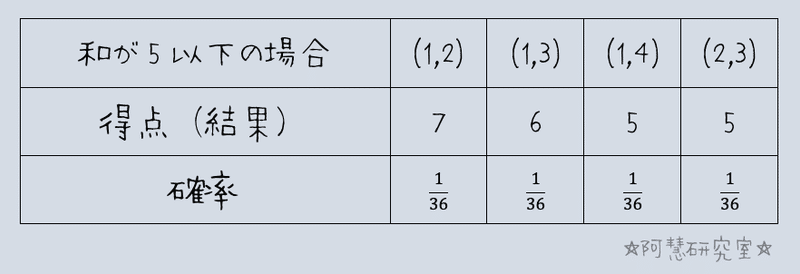
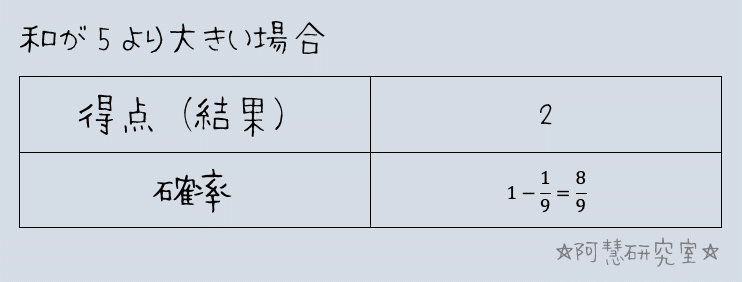
よって，得点の期待値は

---

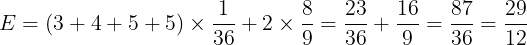
（２）（１）より，１回の試行において，Sが５以下になる確率は

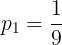
である。
（i）２回ともSが５以下になる確率は

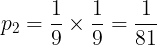
である。
（ii）方法①：「少なくとも１回は，Sが５以下になる」という事象は，「１回目：Sが５以下になる，２回目：Sが５より大きい」，「１回目：Sが５より大きい，２回目：Sが５以下になる」，「２回とも５以下になる」の和事象です。３つのパターンに分けて考えれば，

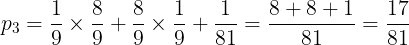
（ii）方法②：「少なくとも１回は，Sが５以下になる」という事象と「２回ともSより大きい」という事象は排反事象であるから，

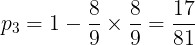
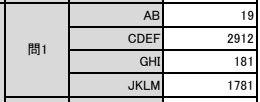
【正解】

解答部分は自作なので，著作権を放棄しておりません。記事をSNS等へシェアしていただけたらすごく嬉しいですが，内容だけを複写・複製・翻訳することは固くお断りします。皆様のご協力をよろしくお願いいたします。

2011年第1回数学コース１の他の問題を見にいく

---

• Twitter

コミュニケーションボックス