※次の解答はただの参考です。必ず自分で探求した後で解答を読むことにしましょう。

【ポイント】

これは，二つの関数のグラフの交点・共通解に関する問題です。

【出題領域】

二次関数。この問題を完璧に解くために，以下の知識が必要です。

（１）「２つの関数が等しくなる」の意味
（２）実数解の存在条件・判別式
（３）二次方程式の解き方（解の公式）
（４）一次不等式の解き方
（５）絶対値を含む不等式の解き方

では，確実に問題を解いてみましょう。

【解答】

（１）二つの関数

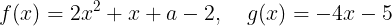
が等しくなるとき，

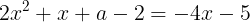
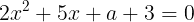
が成り立つ。この二次方程式の実数解の個数を調べれば良い。
上記の二次方程式の判別式は

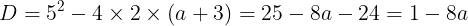
であるから

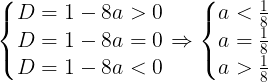
のとき，求める実数xはそれぞれ２つ，１つ，存在しないことになる。

すなわち　⑤のとき，求める実数xは２つ存在する；
　　　　　⑦のとき，求める実数xはただ１つ存在する；
　　　　　①のとき，求める実数xは存在しない。

---

（２）

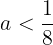
（⑤）のとき，解の公式により，求めるxは

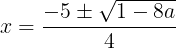
であり，そのときの２つの関数の値は等しく

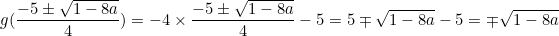
である。

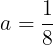
（⑦）のとき，求めるxは

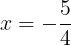
であって，そのときの２つの関数の値は等しく

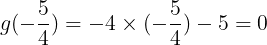
である。

---

（３）（２）より，求めるxにおける２つの関数の値は

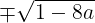
であるから，

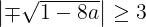
（式＊）を解ければ良い。式＊の両辺ともに２乗して

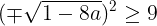
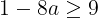
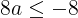
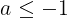
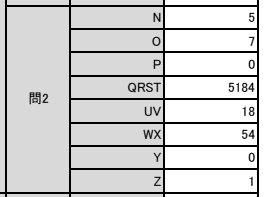
【正解】

解答部分は自作なので，著作権を放棄しておりません。記事をSNS等へシェアしていただけたらすごく嬉しいですが，内容だけを複写・複製・翻訳することは固くお断りします。皆様のご協力をよろしくお願いいたします。

2011年第1回数学コース１の他の問題を見にいく

---

• Twitter

コミュニケーションボックス