※次の解答はただの参考です。必ず自分で探求した後で解答を読むことにしましょう。

【ポイント】

仮定の情報が少ないですね。僅かの情報を数学の言葉で表してみましょう。

【出題領域】

二次関数，（数と式）。この問題を完璧に解くために，以下の知識が必要です。

（１）二次関数の頂点の座標
（２）二次不等式の解き方
（３）無理数の整数部分・小数部分
（４）関数のグラフの平行移動
（５）文字を含む分数が整数になる条件

【関数グラフの平行移動】

では，確実に問題を解いてみましょう。

【解答】

（１）①のグラフの頂点

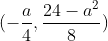
は第１象限にあるから，連立方程式

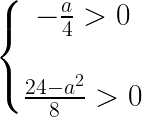
を満たす。つまり，aのとりうる値の範囲は

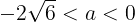
である。また，

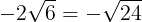
であるから,

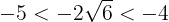
であり，数直線で表すと

となる。よって，この範囲にある最小の整数aは-4である。

---

（２）問題より，a=-4としたとき，式①は

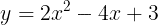
となり，基本形に変形すると

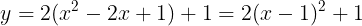
となる。このとき，①のグラフを

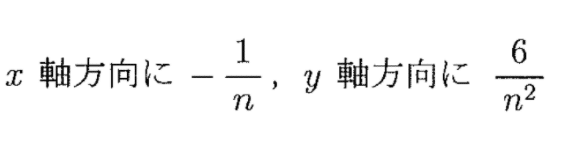
だけ平行移動すると

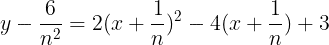
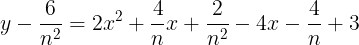
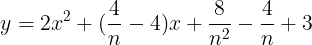
で表すことができる。よって，

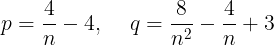
である。

---

（３）（２）において，

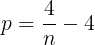
が整数となるとき，すなわち

が整数になるとき，自然数nは４の約数である。したがって，nがとり得る値は

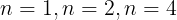
全部で３個ある。これらのnのうちq

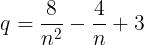
の値も整数となるものを考える。

n=1のとき，

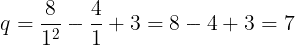
n=2のとき，

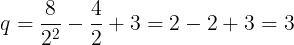
n=4のとき，

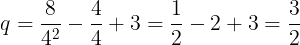
は整数ではないため，条件を満たさない。よって，qが最小となるのはn=2のとき，その値はq=3である。

【正解】

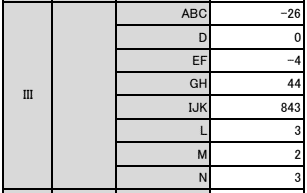
解答部分は自作なので，著作権を放棄しておりません。記事をSNS等へシェアしていただけたらすごく嬉しいですが，内容だけを複写・複製・翻訳することは固くお断りします。皆様のご協力をよろしくお願いいたします。

2011年第1回数学コース１の他の問題を見にいく

---

• Twitter

コミュニケーションボックス