※次の解答はただの参考です。必ず自分で探求した後で解答を読むことにしましょう。

【ポイント】

三角形において，２つの辺と１つの角を知って，残りの一辺を求めるとき，「余弦定理」を使う。三角形の外接円の半径を求めるとき，「正弦定理」を使う。

【出題領域】

図形の性質と計量。この問題を完璧に解くために，せめて以下の知識が必要です。

（１）余弦定理
（２）正弦定理
（３）特殊の角の三角比
（４）解の公式

では，確実に問題を解いてみましょう。

【解答】

（１）線分ACを引く。

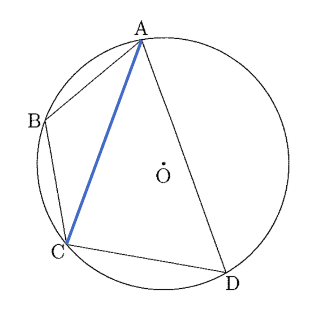
△ABCにおいて，余弦定理により

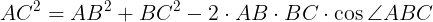
（式＊）が得られ，

を式＊に代入し，

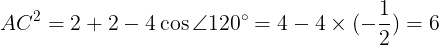
したがって，

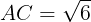
である。また，円Oは△ABCの外接円であるから，正弦定理により

---

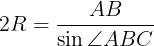
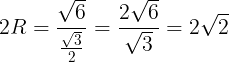
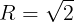
（２）線分BDを引く。

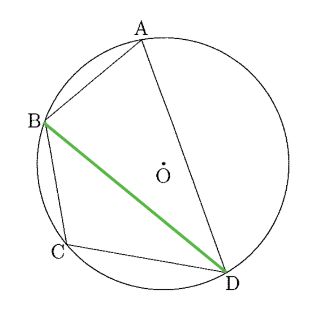
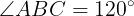
であるから，

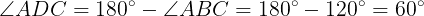
また，

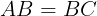
であるから，

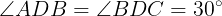
△ABDにおいて，余弦定理により

（式％）が得られ，

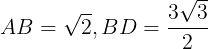
を式％に代入し，

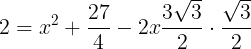
になる。両辺とも４をかけて

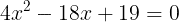
が得られる。同様に，△BCDにおいて，余弦定理により，

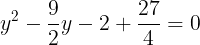
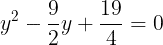
両辺ともに４をかけて

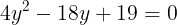
が得られる。
以上より，①に注意すれば，

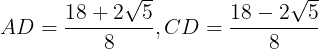
が得られる。

【正解】

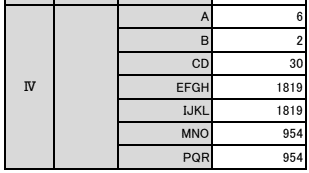
解答部分は自作なので，著作権を放棄しておりません。記事をSNS等へシェアしていただけたらすごく嬉しいですが，内容だけを複写・複製・翻訳することは固くお断りします。皆様のご協力をよろしくお願いいたします。

2011年第1回数学コース１の他の問題を見にいく

---

• Twitter

コミュニケーションボックス