※次の解答はただの参考です。必ず自分で探求した後で解答を読むことにしましょう。

【ポイント】

関数のグラフは原点に関して対称なものを求めるとき，xとyを-xと-yにすればよいです。

【出題領域】

二次関数。この問題を完璧に解くために，せめて以下の知識・技能が必要です。

（１）関数のグラフ
（２）二次関数の軸
（３）二次関数の頂点座標
（４）二次関数の最大値・最小値

では，問題の解答をみましょう。

【解答】

（１）原点に関する対称性から①の二次関数を

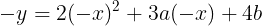
のように変形でき，すなわち①と原点に関して互いに対称である二次関数は

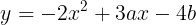
である。この式の係数が②の係数とそれぞれ等しいので，

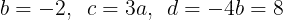
となる。よって，②は

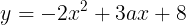
となる。

---

（２）③のグラフの軸は

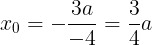
であり，上に凸である。仮定より

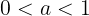
であるから，軸の範囲は

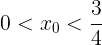
を満たす。また，xの値の範囲（定義域）が

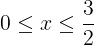
であるから，軸はこの範囲に入っている。よって，③の最大値は

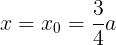
においてとり，

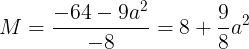
となる。

最小値を求めるのに，２つの考え方がある。
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
その１の考え方：
③の定義域の両端のうち，軸に遠いものにおいては最小値を取る。
定義域の中点は

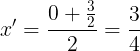
であるから，③の軸はxの定義域の左半分にある。つまり，右端は軸により遠い。よって，最小値は

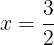
において取り，

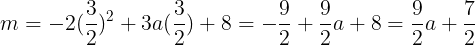
となる。よって，yの値の範囲は

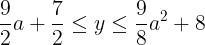
である。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
その２の考え方：
③の最大値は軸において取り，最小値は必ず定義域の両端に取る。それぞれ求めて，大きさを比べればよい。定義域の右端における関数の値は

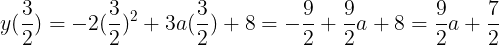
である。

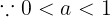
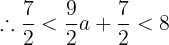
定義域の左端における関数の値は

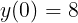
である。よって，前者の値がより小さいので，③の最小値は

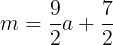
である。よって，yの値の範囲は

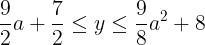
である。

---

（３）③の式よりその頂点の座標は

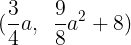
を得られる。この点はつねに二次関数

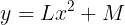
（式④）のグラフにあるとする。頂点の座標を④に代入し，

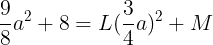
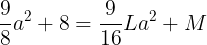
となり，aの２次項の係数と定数項がそれぞれ対応するから

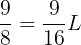
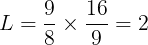
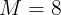
となる。よって，この二次関数の式は

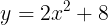
である。

【正解】

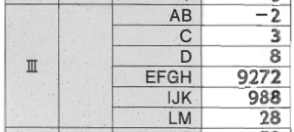
解答部分は自作なので，著作権を放棄しておりません。記事をSNS等へシェアしていただけたらすごく嬉しいですが，内容だけを複写・複製・翻訳することは固くお断りします。皆様のご協力をよろしくお願いいたします。

2011年第2回数学コース１の他の問題を見にいく

---

• Twitter

コミュニケーションボックス