※次の解答はただの参考です。必ず自分で探求した後で解答を読むことにしましょう。

【ポイント】

三角形の面積の求め方に基づいた問題です！三角形の面積の求め方，何通り言えるのでしょうか？

【出題範囲】

図形の性質と計量。この問題を完璧に解くために，せめて以下の知識が必要です。

（１）余弦定理
（２）三角形の面積の求め方
（３）特殊の角の三角比
（４）三角形の面積比

では，問題を解いてから解答をみましょう。

【解答】

（１）

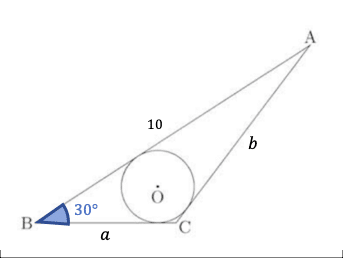
上の図のように，三角形ABCの面積は

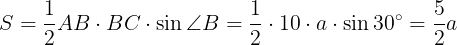
また，下の図のように，三角形ABCを三角形AOB，三角形BOC，三角形AOCに分けて考えると，

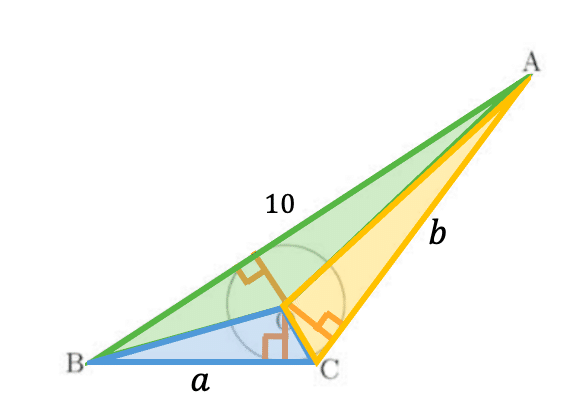
このとき，三角形ABCの面積は

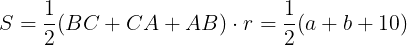
で表せる。したがって，

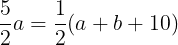
となり，

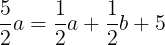
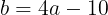
（式①）が成り立つ。三角形ABCにおいて，余弦定理により，

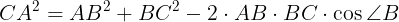
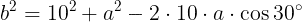
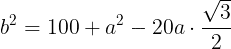
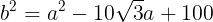
（式②）が成り立つ。式①を式②に代入して

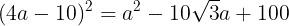
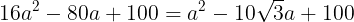
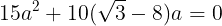
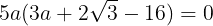
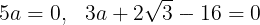
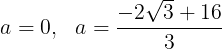
aは長さであり0ではないから

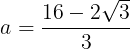
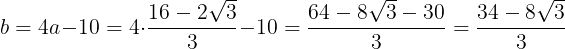
である。

---

（２）問題に従い，線分CDを引く。

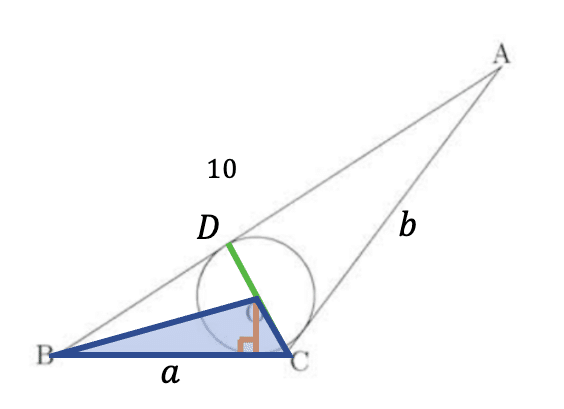
三角形OBCの面積は

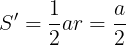
であるから，三角形ABCと三角形OBCの比は

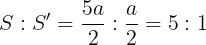
となる。また，下の図のように，点Aを通った線分BCの垂線を引いて，BCを延長した直線とFに交わる。

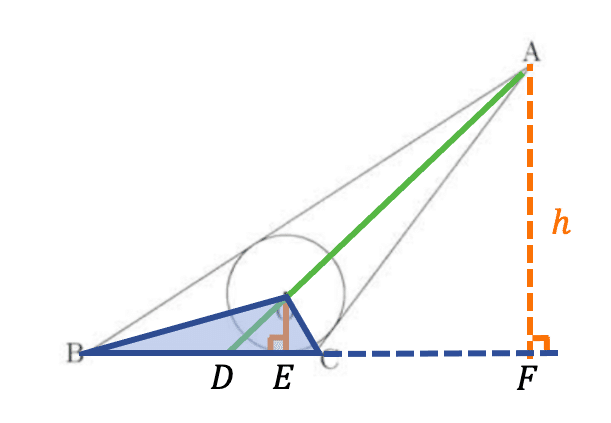
三角形ABCと三角形BOCは，同じくBCを底辺とする三角形である。

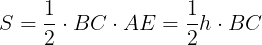
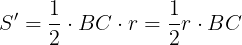
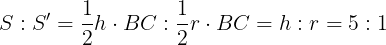
つまり，この二つの三角形について，高さの比＝面積の比となる。

また，∠OED=∠AFD=90°，∠Dは共通だから，

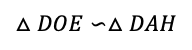
となる。対応する辺の比が等しいので

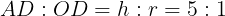
である。よって，

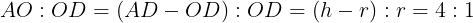
である。

【正解】

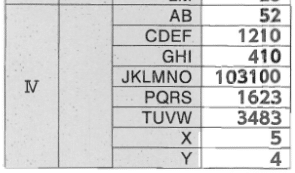
解答部分は自作なので，著作権を放棄しておりません。記事をSNS等へシェアしていただけたらすごく嬉しいですが，内容だけを複写・複製・翻訳することは固くお断りします。皆様のご協力をよろしくお願いいたします。

2011年第2回数学コース１の他の問題を見にいく

---

• Twitter

コミュニケーションボックス