※次の解答はただの参考です。必ず自分で探求した後で解答を読むことにしましょう。

【ポイント】

仮定より，書ける不等式を全部書いておく。そして問題に従って，適切な不等式を選んで，不等式を解けばOK〜

【出題範囲】

二次関数。この問題を完璧に解くために，せめて以下の知識・技能が必要です。

（１）二次関数のグラフの軸
（２）判別式
（３）二次関数のグラフとx軸
（４）共有点の範囲

では，問題を解いてから解答を見ましょう。

【解答】

仮定より，二次関数

のグラフの軸は

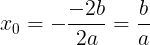
（式①）である。この二次関数のグラフはx軸と共有点を複数持つから，判別式

（式②）が成り立つ。
さらに，共有点はすべて区間0<x<1の中にあるから

• 軸はこの区間にある
• f(0)，f(1)が正，f(軸)が負

がわかる。すなわち

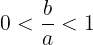
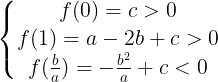
（式③，式④，式⑤，式⑥）となる。

（１）式③

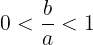
であるから，aとbの大小については

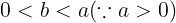
を満たす。←選択肢⓪

---

（２）（１）より

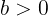
である。また，式④より

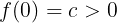
である。←選択肢③

---

（３）式⑤より

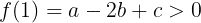
であるから

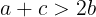
となる。←選択肢①

---

（４）式②

であるから，

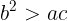
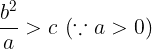
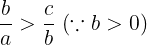
となる。（１）より

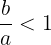
であるから，bとcの大小については

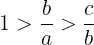
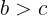
となる。←選択肢⓪

---

（５）以上をまとめ，a，b，cの関係は

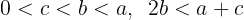
を満たす。
小さい方から考えていく：
c=1，b=2，c=3のとき，2b=a+cであるから，条件を満たさない。
c=1，b=2，c=4のとき，2b<a+cであるから，条件を満たす。
よって，aのとり得る最小の整数は４であり，そのときのbの値は２，cの値は１である。

【正解】

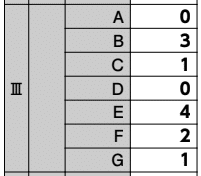
解答部分は自作なので，著作権を放棄しておりません。記事をSNS等へシェアしていただけたらすごく嬉しいですが，内容だけを複写・複製・翻訳することは固くお断りします。皆様のご協力をよろしくお願いいたします。

2013年第1回数学コース１の他の問題を見にいく

---

• Twitter

コミュニケーションボックス