※次の解答はただの参考です。必ず自分で探求した後で解答を読むことにしましょう。
【出題領域】
図形。
【解答】
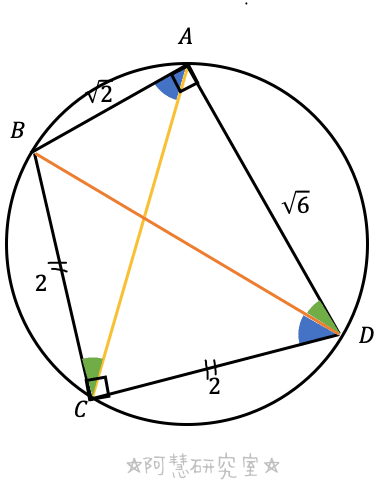
仮定より,図をかいておく。
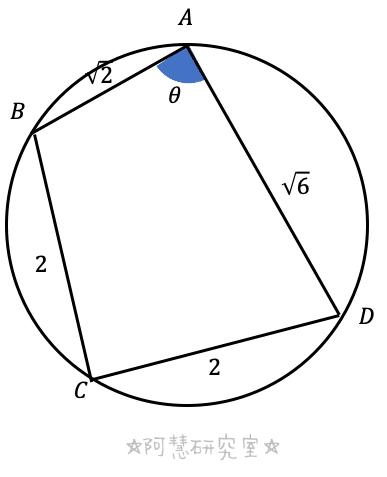
(1)
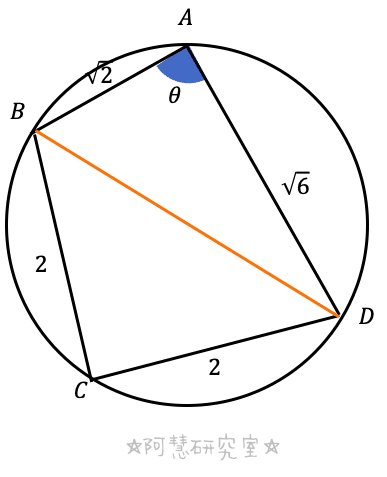
三角形ABDにおいて,余弦定理により
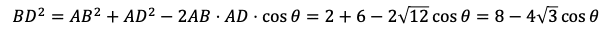
がわかる。また,三角形BCDにおいて,余弦定理により
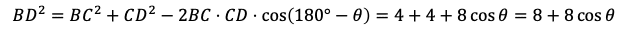
を得る。よって,
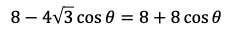
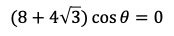
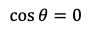
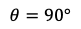
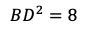
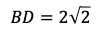
※ちなみに,θ=90°であるからBDは直径である。
(2)
円の内接四角形の性質より
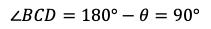
であり,それに
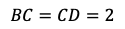
であるから,三角形BCDは直角二等辺三角形である。よって,
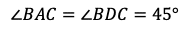
である。さらに,円周角の定理により,∠BCA=∠BDAであるから
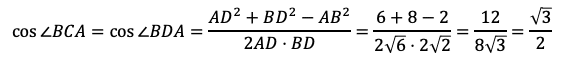
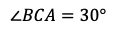
となる。
三角形ABCにおいて,余弦定理により
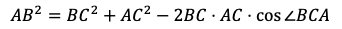
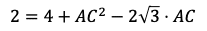
となる。x=ACとおいて,xについての二次方程式
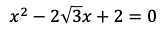
を解く。解の公式より
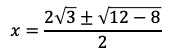
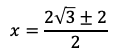
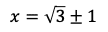
となる。三角形の成り立つ条件により,
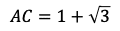
である。三角形ACDにおいて,正弦定理により
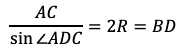
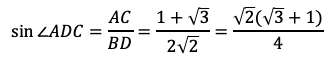
である。
sin∠ADCの値については,別解がある。
方法二:
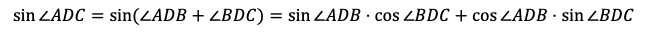
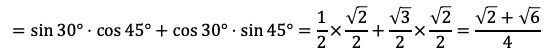
(3)仮定より,下の図をかける。
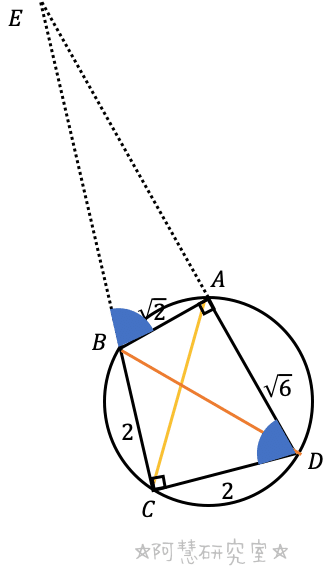
直角三角形EABにおいて,三平方の定理により
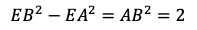
(式①)が得られる。また,三角形EAB∽三角形ECDであるから,
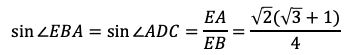
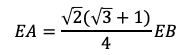
である。これを式①に代入してEBを求めることができるので,まずはEAの2乗を計算して
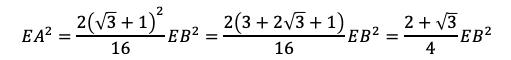
となり,①に代入して
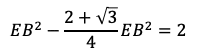
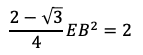
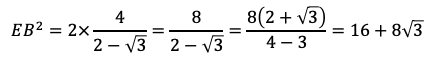
である。よって,
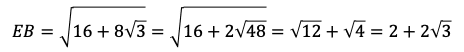
である。

【正解】

解答部分は自作なので,著作権を放棄しておりません。記事をSNS等へシェアしていただけたらすごく嬉しいですが,内容だけを複写・複製・翻訳することは固くお断りします。皆様のご協力をよろしくお願いいたします。
2014年第2回数学コース1の他の問題を見にいく
コミュニケーションボックス

