
#94・2018年第1回 大問1-2【EJU解答】
【出題領域】
場合の数と確率。この問題を完璧に解くために,せめて以下の知識・技能が必要です。
(1)和の法則
(2)積の法則
では,問題を解いてから解答を見ましょう。
【解答】
大きさの異なる4枚のカードがあり,赤,黒,青,黄色を塗る。
(1)どのカードにも4種類の色を塗ることができるから,全部で
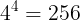
通りある。
(2)全部の色を使う塗り方は
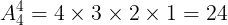
通りある。
(3)同じ色(赤)を塗るカードを取り出す:

である。残りの2枚の塗り方は

である。よって,求める2枚は赤で,1枚が黒,1枚が青となるような塗り方は
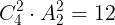
通りある。
(4)3つの色を使うから,まず3つの色を選ぶ:
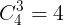
通りの色の選び方がある。そして,4つのカードに塗る。このとき,同じ色を塗るカードが2枚あるので,(3)と同様に,同じ色を塗るカードを1つのグループとして考える。3グループのカードに色を塗る仕方は
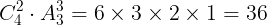
通りである。よって,求める塗り方は3つの色を使う塗り方は
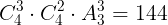
通りある。
(5)2つの色を使って塗るから,まずは2つの色を選ぶ:
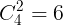
通りある。
さらに,このとき,同じ色で塗られたカードは以下の3つの場合があり,
A色 B色
・場合①:(3枚,1枚)
・場合②:(2枚,2枚)
・場合③:(1枚,3枚)
計

通りある。よって,求める2つの色を使う塗り方は
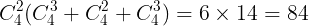
通りある。
※順列で考えるとき,場合①と場合③をまとめて考えることも可。

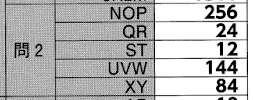
【正解】

解答部分は自作なので,著作権を放棄しておりません。記事をSNS等へシェアしていただけたらすごく嬉しいですが,出処省略し内容だけを複写・複製・翻訳することは固くお断りします。皆様のご協力をよろしくお願いいたします。
