
#96・2018年第1回 大問2-2【EJU解答】
【出題領域】
二次関数。この問題を完璧に解くために,せめて以下の知識・技能が必要です。
(1)二次関数のグラフとx軸の交点
(2)判別式
(3)二次関数の定義域と値域
(4)二次方程式・二次不等式の解き方
すごく典型的な問題なので,ぜひ身につけておきましょう!
では,問題を解いてから解答を見ましょう。
【解答】
(1)f(x)=0とg(x)=0の解が一致するから以下の2つのことを言える。
- f(x)とg(x)の交点が2つある
- f(x)とg(x)の軸は同じである
1.について,f(x)とg(x)を連立して
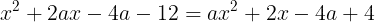
を得る。整理してxについての二次方程式

が得られる。この二次方程式は2つの解があるから

が成り立つ。よって,aの値の範囲は
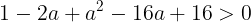
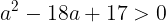

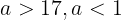
を満たす。そして,2.について,f(x)とg(x)の軸それぞれは
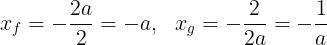
であり,等しいから



となる。1.の結果により,aは
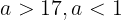
であるから,
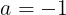
である。このとき,
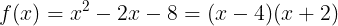
となり,f(x)=0は次のようになる。
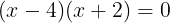
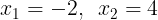
※解が共通であるから,g(x)で解いてもOKです。ただ,両方とも解く必要はない(←確認時にやればOK)。
(2)g(x)重解をもつから,判別式D=0となる。すなわち
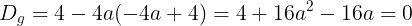
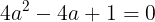
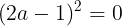
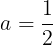
となる。また,その重解はg(x)のグラフの頂点座標のx座標(軸の方程式)である。このとき,
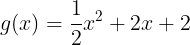
であり,軸の方程式は
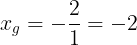
となる。よって,そのときの解は

である。
(3)すべてのxに対して,
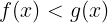
が成り立つということは,
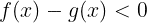
である。新しい関数
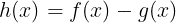
で考えると,すべてのxに対して値域が0より小さいh(x)を求めることとなる。関数h(x)は
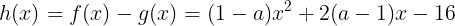
であり,必ずしも二次関数であることは言えないので,場合を分けてやっていく。
h(x)は一次関数である場合:
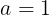
となり,
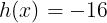
であるから,すべてのxに対してh(x)<0を満たす。
h(x)は2次関数である場合:「すべてのxに対してh(x)の値域が0より小さい」ということは
- x軸と交わらない
- 上に凸(あるいは頂点のy座標は0より小さいことで考えても可)
のことである。すなわち,D<0かつ(1-a)<0となる。
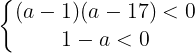
よって,aの範囲は
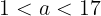
となる。h(x)は一次関数である場合とh(x)は二次関数である場合をまとめて,aの値の範囲は
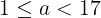
である。

【正解】
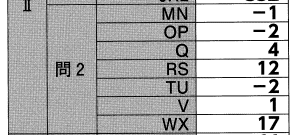

解答部分は自作なので,著作権を放棄しておりません。記事をSNS等へシェアしていただけたらすごく嬉しいですが,出処省略し内容だけを複写・複製・翻訳することは固くお断りします。皆様のご協力をよろしくお願いいたします。
