☆阿慧研究室☆

【ポイント】

ぱっっと見れば難しそうな感じがするかもしれないが，問題よりかなりのヒントが与えられた。それに従って，どんどん解けて，欲しいものが得られるよ！逃げずにやって行こう！

【出題領域】

整数の性質（数と式も少し）。この問題を完璧に解くために，せめて以下の知識・技能が必要です。

（１）因数分解
（２）連続する自然数の性質
（３）約数と倍数
（４）素数

では，問題を解いてから解答を見ましょう。

【解答】

条件より，

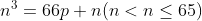
と表せる。これを変形して

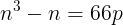
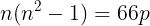
（式①）を得る。
　ここで，n-1，nは二つの連続の自然数であるから，どちらか一方は２の倍数，n-1，n，n-1は三つの連続の自然数であるから，そのうち１つは３の倍数である。２と３は互いに素であるから，

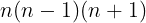
は6の倍数である。このことは，式①からも得られる。式①は

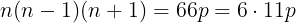
に整理でき，すなわち

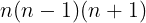
は６の倍数かつ11の倍数である。６と11も互いに素であるから，
n-1，n，n+1のいずれか１つが11の倍数となる場合を考えればよい。

いま，

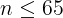
である。
場合①：n-1が11の倍数であるものは

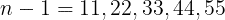
である。よって，nは

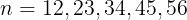
計５個ある。
場合②：nが11の倍数であるものは

計５個ある。
場合②：n+1が11の倍数であるものは

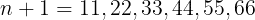
である。よって，nは

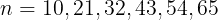
計６個ある。

以上をまとめ，求めるnの個数は５＋５＋６＝１６個であり，このうち，素数であるnは小さい順に，

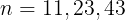
である。

【正解】

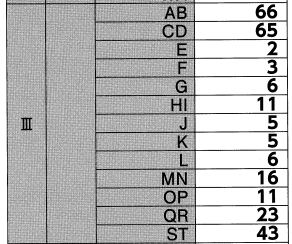
解答部分は自作なので，著作権を放棄しておりません。記事をSNS等へシェアしていただけたらすごく嬉しいですが，出処省略し内容だけを複写・複製・翻訳することは固くお断りします。皆様のご協力をよろしくお願いいたします。