☆阿慧研究室☆

#98・2018年第1回　大問4【EJU解答】

【出題領域】

図形。この問題を完璧に解くために，せめて以下の知識・技能が必要です。

（１）三角比
（２）三平方の定理
（３）方べき定理
（４）三角形の面積

では，問題を解いてから解答を見ましょう。

【解答】

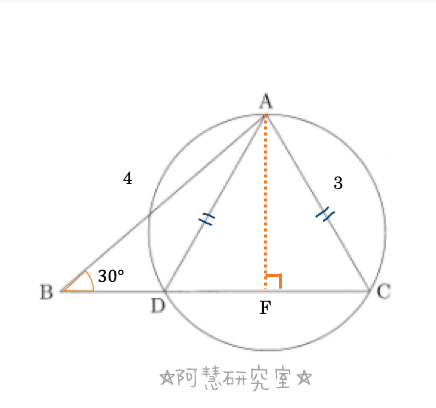
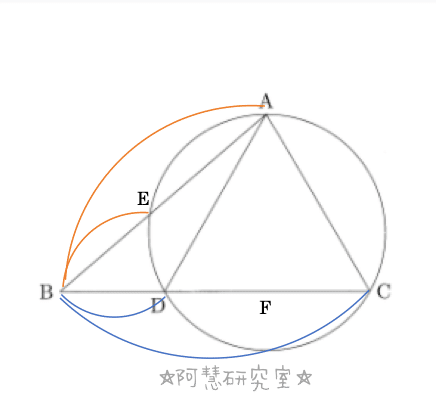
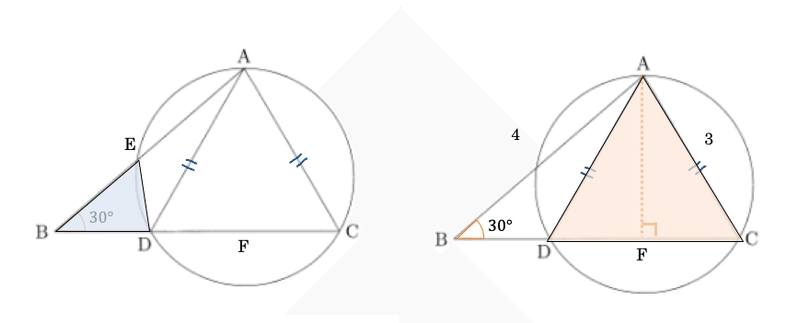
（１）線分DCの中点を点Fとし，線分AEを引く（下の図になる）。AD＝ACであるから，AF⊥DCとなる。

仮定より

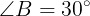
であるから

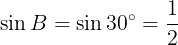
である。直角三角形AEBにおいて，三角比の定義により

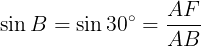
であるから

が得られる。また，直角三角形AECにおいて，三角比の定義により

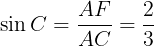
である。したがって，正弦定理により，三角形ADCの外接円の半径は

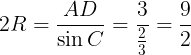
である。

（２）三角形ABCにおいて，

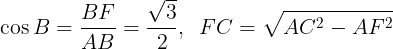
が成り立つ。

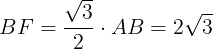
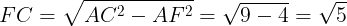
よって，

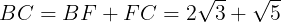
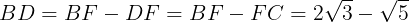
が得られる。方べき定理により，BD・BC＝AB・BEが成り立つ。

よって，

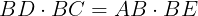
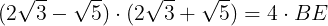
である。

さらに，△BDEと△ADEは同じ高さをもつ三角形であるから，面積比の比はそれらの底辺の比となる。よって，

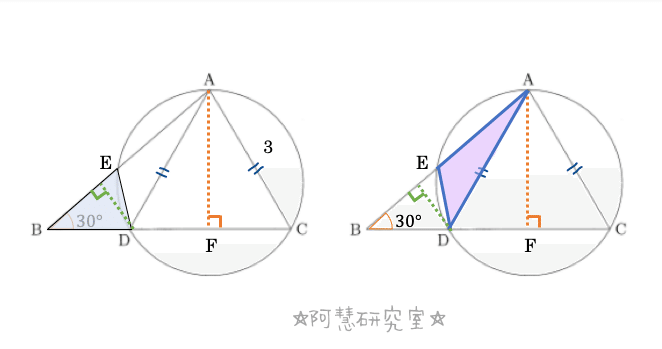
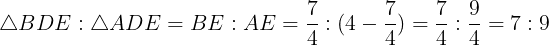
である。
また，△BDEと△ACDの面積それぞれは

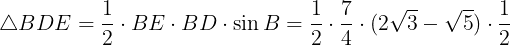
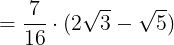
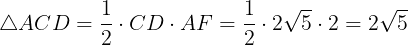
であるから，

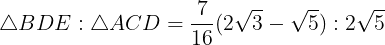
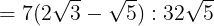
が成り立つ。

【正解】

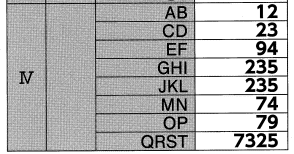
解答部分は自作なので，著作権を放棄しておりません。記事をSNS等へシェアしていただけたらすごく嬉しいですが，出処省略し内容だけを複写・複製・翻訳することは固くお断りします。皆様のご協力をよろしくお願いいたします。

2018年第1回数学コース１の他の問題を見にいく