※次の解答はただの参考です。必ず自分で探求した後で解答を読むことにしましょう。

【ポイント】

問（１）と問（２）は別々の仮定に基づいた問いなので，ご注意ください。この問題の難点は，たすきがけによる因数分解だと思います！

【出題範囲】

数と式（整数の性質）。この問題を完璧に解くために，せめて以下の知識・技能が必要です。

（１）有理数と無理数の性質
（２）因数分解：たすきがけ
（３）素数になる条件

では，問題を解いてから解答を見ましょう。

【解答】

（１）問題より

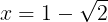
を

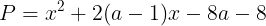
に代入し

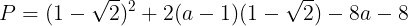
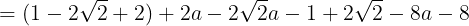
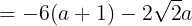
が得られる。有理数と無理数の性質により，Pの値が有理数になるのは

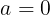
のときであり，そのときのPの値は

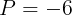
である。

---

（２）Pを因数分解する。

つまり，Pを因数分解して

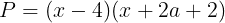
を得る。Pの値が素数になるように，

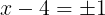
とし，すなわち

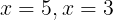
になる。
場合１：

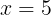
のとき，Pは

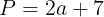
になる。さらに，

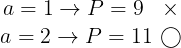
であるから，Pの値が素数になるようなaの最小値は11である。
場合２：

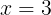
のとき，Pは

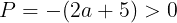
になり，Pは正の整数になるために

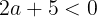
が必要である。しかし，aも正の整数であるため，上の式を満たすaはない。よって，場合２はこの問題を満たさない。

【正解】

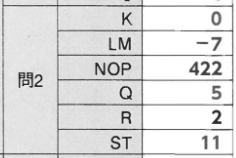
解答部分は自作なので，著作権を放棄しておりません。記事をSNS等へシェアしていただけたらすごく嬉しいですが，内容だけを複写・複製・翻訳することは固くお断りします。皆様のご協力をよろしくお願いいたします。

2012年第1回数学コース１の他の問題を見にいく

---

• Twitter

コミュニケーションボックス