※次の解答はただの参考です。必ず自分で探求した後で解答を読むことにしましょう。

【ポイント】

この問題は確率を背景とした動点問題です。規則に従い，点の動かし方によって確率をそれぞれ書いておくのは下準備です。

【出題範囲】

場合の数と確率。この問題を完璧に解くために，せめて以下の知識・技能が必要です。

（１）サイコロモデル：出た目（根元事象）の確率
（２）独立試行と反復試行

では，問題を解いてから解答を見ましょう。

【解答】

（１）１個のサイコロを1回投げて，３の倍数の目が出る確率は

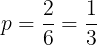
３の倍数の目が出ない確率は

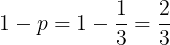
サイコロを4回投げて（反復試行だよ），点Pが点（３，１）に到達するように，３の倍数である目が３回，３の倍数でない目が1回が出るのが必要です。

よって，求める確率は

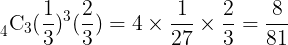
である。

---

（２）サイコロを４回投げる。４回のうち，３の倍数の目が出る回数は

の５通りがあるから，Pが到達し得る点は全部で５個ある。
３の倍数の目が出ない場合，もちろん３の倍数でない目が出る。そのため，これらの点の座標はそれぞれ

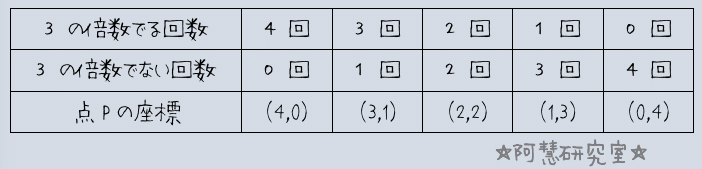
になり，まとめて整数kを用いて

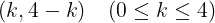
と表すことができる。

このとき，Pが点（k,4-k）に到達する確率はそれぞれ

であり，最大値は

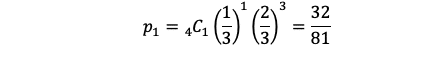
最小値は

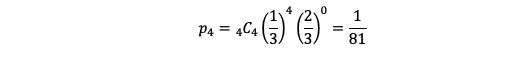
である。

---

（３）原点から点（１，１）に到達する確率は

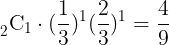
であり，点（１，１）から点（２，２）に到達する確率は

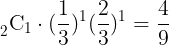
である。よって，求める確率は

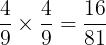
である。

【正解】

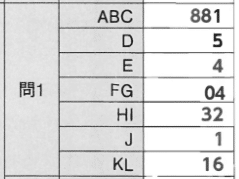
解答部分は自作なので，著作権を放棄しておりません。記事をSNS等へシェアしていただけたらすごく嬉しいですが，内容だけを複写・複製・翻訳することは固くお断りします。皆様のご協力をよろしくお願いいたします。

2012年第1回数学コース１の他の問題を見にいく

---

• Twitter

コミュニケーションボックス