※次の解答はただの参考です。必ず自分で探求した後で解答を読むことにしましょう。
【出題領域】
関数のアイデアを使った二次不等式の問題です。
【3乗に関係する因数分解】
以下の5つがあります〜!特に基本対称式のものを覚えといてくださいね。
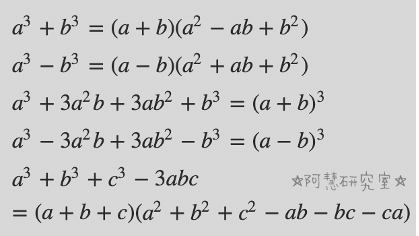
では,問題を解いてから解答を見ましょう。
【解答】
不等式①の左辺は平方完成の形に変形すると
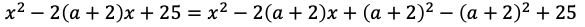
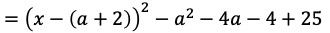
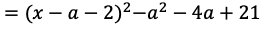
になる。
(1)不等式①は
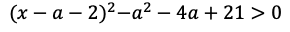
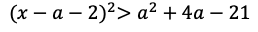
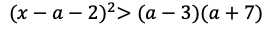
になる。左辺の二次関数の最小値は
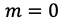
であるから,最小値でも右辺の値より大きかったらよい。よって,
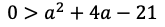
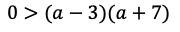
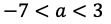
である。
(2)不等式①がx≧-1を満たすすべての実数xに対して成り立つことはx≧-1の範囲では,左辺の二次関数の最小値は右辺よりも大きいことである。左辺の二次関数を
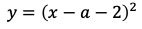
と表し,軸の方程式は
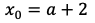
である。
・場合①:
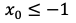
すなわち
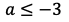
のとき,二次関数の最小値は
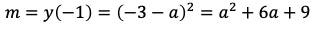
である。このとき,
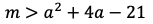
が成り立つから,
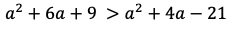
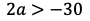
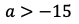
が得られる。よって,条件を満たすaの値の範囲は
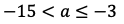
になる。
・場合②:
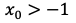
すなわち
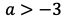
のとき,二次関数の最小値は
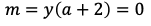
である。このとき,
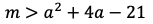
が成り立つから,
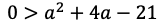
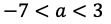
が得られる。よって,条件を満たすaの値の範囲は
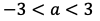
になる。場合①と場合②をまとめてaの値の範囲は
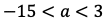
である。

【正解】
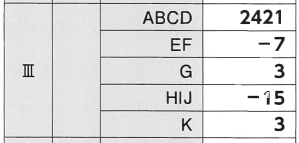

解答部分は自作なので,著作権を放棄しておりません。記事をSNS等へシェアしていただけたらすごく嬉しいですが,内容だけを複写・複製・翻訳することは固くお断りします。皆様のご協力をよろしくお願いいたします。
2013年第2回数学コース1の他の問題を見にいく
コミュニケーションボックス

