※次の解答はただの参考です。必ず自分で探求した後で解答を読むことにしましょう。

【出題領域】

場合の数と確率。

【解答】

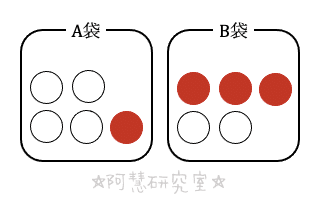
Aから同時に２個の球，Bから同時に２個の球を取り出す場合の数は

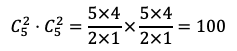
通りある。

---

（１）Aから２個の白球を取り出す場合の数は

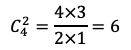
通りある。Bから１個の白球と１個の赤球を取り出す場合の数は

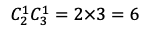
通りある。よって，求める確率は

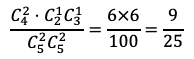
である。

---

（２）取り出した４個の球の中に，３個の白球と１個の赤球があることは２つのパターンに分けられる。

1. 赤球がAから取り出された場合
2. 赤球がBから取り出された場合

赤球がAから取り出されたとき，

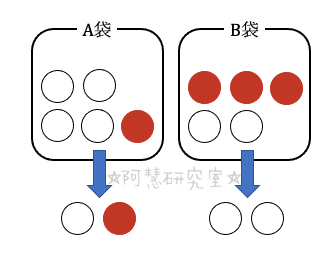
Aから白球と赤球を１つずつ取り出し，Bから２つの白球を取り出す場合の数は

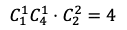
通りある。
赤球がBから取り出されたとき，

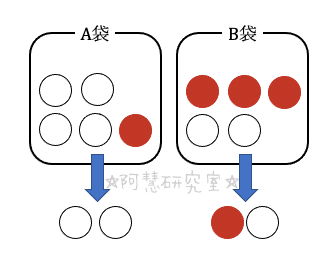
Aから２つの白球取り出し，Bから白球と赤球を１つずつ取り出す場合の数は

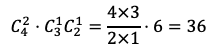
通りある。よって，求める確率は

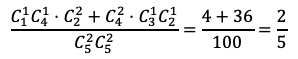
である。

---

（３）取り出す４個の球がすべて同じ色であるとき，白球しかありえない。A，Bとも２個の白球を取り出す場合の数は

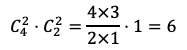
通りある。よって，求める確率は

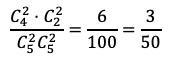
である。

---

（４）取り出した４個の球がすべて白球であることがないから，４個の球の中に含まれる白球が２個以下である確率は

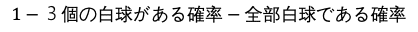
で求められる。よって，求める確率は

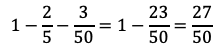
である。

【正解】

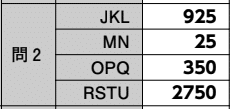
解答部分は自作なので，著作権を放棄しておりません。記事をSNS等へシェアしていただけたらすごく嬉しいですが，内容だけを複写・複製・翻訳することは固くお断りします。皆様のご協力をよろしくお願いいたします。

2015年第1回数学コース１の他の問題を見にいく

---

• Twitter

コミュニケーションボックス