※次の解答はただの参考です。必ず自分で探求した後で解答を読むことにしましょう。

【出題領域】

二次関数。

【解答】

（１）仮定より，一方の放物線がA，B，Cを通り，もう一方はB，C，Dを通ることから，２つの放物線のグラフは下のようになる。

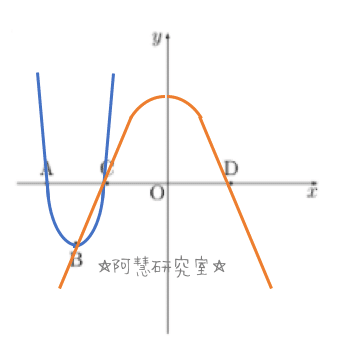
さらに，

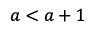
であるから，

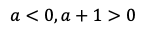
がわかる。よって，点A，B，Cを通る下に凸放物線（青）は

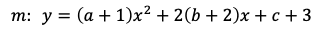
（選択肢：①）であり，点B，C，Dを通る上に凸放物線（オレンジ）は

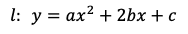
である。

---

（２）放物線l，mの共通点は方程式

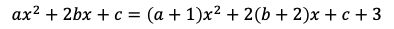
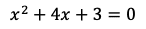
を満たす。xについての２次方程式

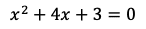
を解くと，

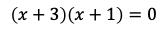
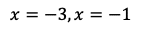
が得られる。よって，点Bのx座標は−３，点Cのx座標は−１である。

---

（３）特に，AB＝AC，CO＝ODのとき，

• 点Bは放物線mの軸にある→直線x＝−３が放物線mの軸である。
• x軸は放物線lの軸である。

ことがわかる。よって，

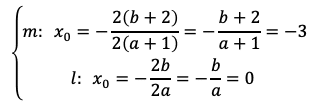
が成り立ち，すなわち

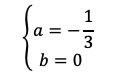
が得られる。よって，放物線lは

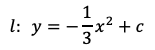
であり，点C（−１，０）を通るから

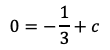
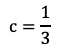
である。

【正解】

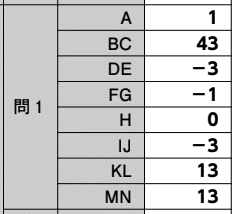
解答部分は自作なので，著作権を放棄しておりません。記事をSNS等へシェアしていただけたらすごく嬉しいですが，内容だけを複写・複製・翻訳することは固くお断りします。皆様のご協力をよろしくお願いいたします。

2015年第1回数学コース１の他の問題を見にいく

---

• Twitter

コミュニケーションボックス