※次の解答はただの参考です。必ず自分で探求した後で解答を読むことにしましょう。
【出題領域】
図形。
【解答】
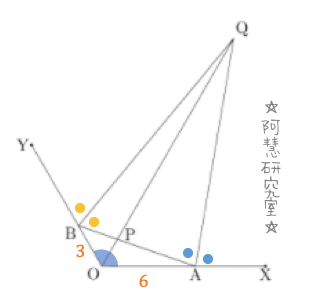
(1)三角形AOBにおいて,余弦定理により
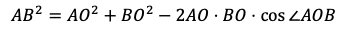
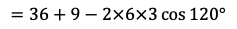
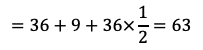
であるから
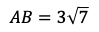
である。よって,三角形OABの面積
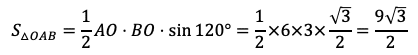
である。
(2)三角形BOPにおいて,BQは∠ABYの二等分線である。外角の二等分線定理により,
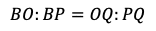
が得られる。また,三角形AOPにおいて,AQは∠BAXの二等分線である。外角の二等分線定理により,
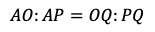
が得られる。よって,
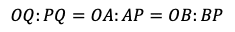
(F:選択肢①,G:選択肢③)が成り立つ。
(3)
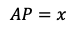
とする。よって,(2)の結果は
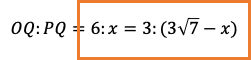
となり,
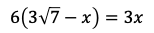
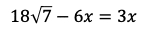
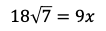
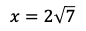
である。よって,
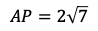
である。
また,Qは角の外角の2等分線の交点であるから,OQは∠AOBの二等分線であり,
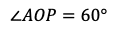
である。余弦定理により
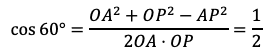
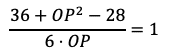
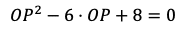
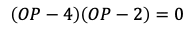
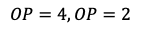
となる。そのうち
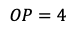
は三角形の辺の成り立つ条件を満たさないから,OP=2となる。
さらに,
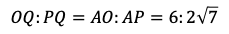
であるから
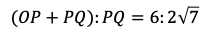
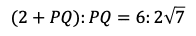
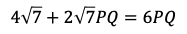
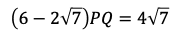
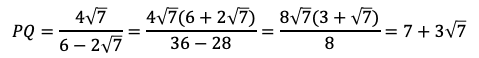
となる。

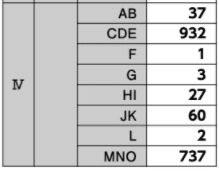
【正解】

解答部分は自作なので,著作権を放棄しておりません。記事をSNS等へシェアしていただけたらすごく嬉しいですが,内容だけを複写・複製・翻訳することは固くお断りします。皆様のご協力をよろしくお願いいたします。
2015年第1回数学コース1の他の問題を見にいく
コミュニケーションボックス

